Το (άλυτο) “Δήλιον πρόβλημα” κι ο Ομάρ Καγιάμ

“Για να γνωρίσω το μυστήριο της ζωής
κούπας τα χείλη άγγιξα, πήλινης, φτωχιάς.
Χείλος στο χείλος μου ψιθύρισε: ‘Όσο ζεις πίνε!
Τι σαν πεθάνεις, δεν ξαναγυρνάς.”
Ομάρ Καγιάμ
Υπάρχουν πολλά άλυτα προβλήματα στα Μαθηματικά. Άλλα είναι απλώς δύσκολα,δηλαδή δεν έχει βρεθεί ακόμη η σωστή προσέγγιση που θα τα επιλύσει, άλλα είναι πιθανώς άλυτα εκ φύσεως, άλλα είναι άλυτα στα πλαίσια μιας συγκεκριμένης αντιμετώπισης που υπακούει υποχρεωτικά σε κάποια προδιαγραφή-νόρμα επίλυσης. Υπάρχει ένα τέτοιο πρόβλημα, που συν των άλλων έχει και θεϊκή προέλευση!
Το πρόβλημα του διπλασιασμού του κύβου, το έθεσε ο ίδιος(σχεδόν..) ο εκηβόλος Φοίβος-Απόλλων στους κατοίκους της Δήλου, οι οποίοι ανήμποροι οι τάλανες να το αντιμετωπίσουν κατέφυγαν στον σοφό Πλάτωνα, μέσω του μαντείου των Δελφών.
Ο ημιμύθος λοιπόν λέει ότι γύρω στο 430 π.Χ μια φονική επιδημία μάστιζε το κυκλαδίτικο ιερό νησί και οι Δήλιοι κατέφυγαν στο μαντείο για να πάρουν έναν σωτήριο χρησμό-οδηγία. Το μαντείο αποφάνθηκε ότι για να τελειώσει το μαρτύριό τους έπρεπε να δείξουν λίγη περισσότερη γενναιοδωρία προς τον Απόλλωνα, αυξάνοντας το μέγεθος ενός κυβικού βωμού που του είχαν ήδη αφιερώσει, και μάλιστα όχι αυθαίρετα, αλλά έπρεπε να τον διπλασιάσουν ακριβώς!
Υπακούοντας στον χρησμό, όντως διπλασίασαν την ακμή του κύβου και έφτιαξαν έναν μεγαλύτερο βωμό, αποδεικνύοντας την ευσέβειά τους αλλά και την μαθηματική ασχετοσύνη τους! Και τα μικρά παιδιά ,στις μέρες μας βέβαια, ξέρουν ότι αν διπλασιαστεί η αρχική ακμή, έστω α, παίρνουμε έναν, όχι διπλάσιο, αλλά οκταπλάσιο κύβο.
(2α)3=8α3=8⋅V αρχικό.
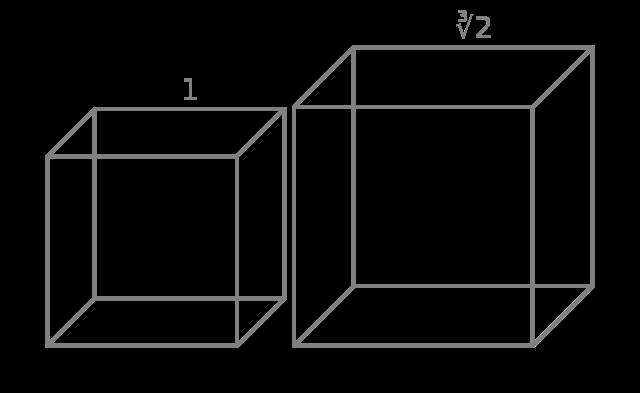
Ο Απόλλων ήταν δυσαρεστημένος. Η ασθένεια συνέχισε να μαστίζει το νησί. Οι κάτοικοι, μαθημένοι πια στους διφορούμενους χρησμούς, κατέφυγαν για τη λύση του προβλήματός τους στον ξακουστό σοφό (και γεωμέτρη) Πλάτωνα τον Αθηναίο. Αυτός τους αποπήρε,όπως μάλλον τούς άξιζε! Αυτό που είχε ζητήσει το μαντείο δεν ήταν διπλάσια ακμή,αλλά διπλάσιος όγκος.
Συγκεκριμένα , έναν βωμό που η νέα του ακμή έστω α’, και ο νέος όγκος του ,έστω V’, θα ικανοποιούσαν τη σχέση: V′=α′3=2V=2⋅α3.
Ή ισοδύναμα: α′=2–√3⋅α
Αυτό λοιπόν που απαιτούσε ο θεός ήταν ένας βωμός με ακμή “τρίτη ρίζα του 2” φορές μεγαλύτερη.
Και ο σοφός Πλάτων κατέληξε ότι αυτό που ήθελε -κατά βάθος- ο θεός, εκφρασμένο μέσω του μαντείου, δεν ήταν βωμοί και μεγαλεία ,αλλά να ασχοληθούν λίγο περισσότερο με τα Μαθηματικά οι Δήλιοι , καθότι οι γεωμετρικές τους γνώσεις ήταν μάλλον θλιβερές.
Γνωρίζοντας λοιπόν το πρόβλημα,το οποίο όπως είδαμε ανάγεται στην γεωμετρική κατασκευή της τρίτης ρίζας του δύο, μπορούμε να υποθέσουμε ότι ο Απόλλωνας φάνηκε τελικά μεγαλόψυχος και απάλλαξε τους κατοίκους από τη μάστιγα, ή, κάπως πιο ρεαλιστικά, ότι η ασθένεια τελικά θεραπεύτηκε από μόνη της , καθώς το γνωστό από τότε ως “Δήλιον πρόβλημα” δεν έχει λύση , όπως απέδειξε, μόλις το 1837, ο Pierre Wantzel.
To Δήλιο πρόβλημα, ο διπλασιασμός του κύβου, απαιτεί χρήση μόνο “Κανόνα και διαβήτη” σύμφωνα με τα αυστηρά γεωμετρικά πρότυπα των Ελλήνων. Κι όταν λέμε “κανόνα”, δεν εννοούμε υποδεκάμετρο/χάρακα με σημάδια. Και επιπροσθέτως ,ο αριθμός των διακριτών βημάτων πρέπει να είναι πεπερασμένος. Η ελληνική νόρμα, εκφρασμένη μέσα από το αξιωματικό σύστημα του Ευκλείδη, φαντάζει και είναι δύστροπη, αλλά έχει τη λογική της. Το να μην επιτρέπεται να χαραχτούν σημάδια στον κανόνα, έχει την έννοια του να μην μπορεί να προκαθοριστεί μια “μονάδα μέτρησης” πάνω στον κανόνα. Και αν αυτό ακούγεται κάπως φιλοσοφικό και αφηρημένο, ας σκεφτούμε τη σχετικότητα των “μονάδων μέτρησης” και των συστημάτων τους διαχρονικά.
Ο περιορισμός πάλι για πεπερασμένο αριθμό βημάτων είναι πιο “γήινος” και πηγάζει μάλλον από τον σεβασμό και την προσοχή ,αν όχι δέος, με τον οποίον αντιμετώπιζαν την έννοια του απείρου, και οπωσδήποτε από την κοινή λογική!
Ποιος εχέφρων άνθρωπος (και αυτοί οι “Παλαιοί” ήταν αρκούντως εχέφρονες) θα εκτελέσει άπειρες ας πούμε διχοτομήσεις μιας γωνίας; Για να θυμηθούμε έτσι κι άλλο ένα διάσημο άλυτο πρόβλημα της αρχαιότητας, την τριχοτόμηση της γωνίας. Αν ας πούμε διχοτομήσουμε (είναι πολύ εύκολο με κανόνα και διαβήτη) μία γωνία α, και συνεχίσουμε τις διχοτομήσεις “επ’ άπειρον”, παίρνουμε διαδοχικά γωνίες μέτρου α/2 , α/4, α/8,…, α/2^ν,… κι αν αθροίσουμε την ακολουθία:
α/4 + α/16 + α/64 +…+α/4^ν = α/3 … κι έχουμε τριχοτομήσει τη γωνία, μόνο που έχουμε καταστρατηγήσει τον κανόνα των πεπερασμένων βημάτων, και την κοινή λογική.

Delian Problem Or Doubling Cube Equivalence Among Various Parts Of Circle From Atlantic Codex Painting by Leonardo da Vinci
Επανερχόμενοι λοιπόν στο “Δήλιο πρόβλημα”, υπάρχουν πολλοί έξυπνοι τρόποι να λυθεί γεωμετρικά αλλά κανείς που να πληρεί την αυστηρή ελληνική νόρμα.Ασχολήθηκαν μεγάλα ονόματα των Μαθηματικών με το πρόβλημα.
Ο Αρχύτας (428-347 π.Χ), ο Μέναιχμος (380-320 π.Χ), ο Φίλων ο Βυζάντιος(280-220 π.Χ) , ο Νικομήδης (280-210 π.Χ), ο Διοκλής (240-180 π.Χ) και ο Ήρων ο Αλεξανδρινός (10-75 μ.Χ) , δώσανε λύσεις του προβλήματος. Όλες όμως αυτές οι λύσεις κάνουν χρήση κανόνα και διαβήτη χωρίς να τηρούνται οι απαραίτητοι περιορισμοί.
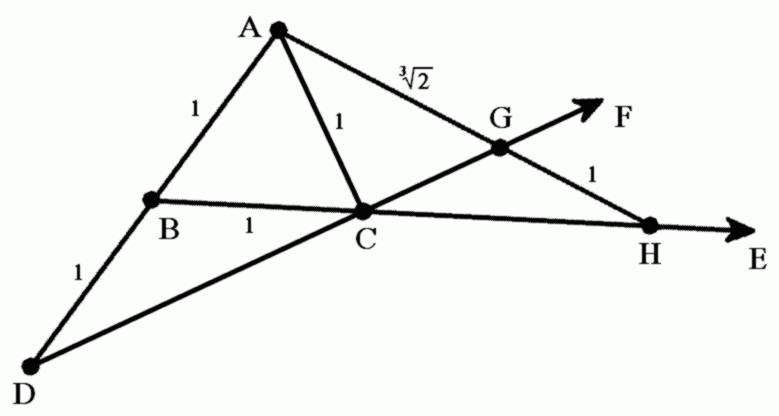
Ακόμη και μια ευφυής λύση,που αποδίδεται στον “πολύ” Ισαάκ Νεύτωνα, και φαίνεται πιο κάτω,απαιτεί να σημειωθεί η ακμή του κύβου πάνω στο χάρακα.
Στο σημείο αυτό, θα μπλέξουμε στην ιστορία μας και τον σπουδαίο Πέρση μαθηματικό (και με πολλές άλλες ιδιότητες ταυτόχρονα) και σοφό Ομάρ Καγιάμ.
Ένα από τα γνωστότερα μαθηματικά επιτεύγματα του Καγιάμ ήταν η εύρεση γεωμετρικών κατασκευών για τις ρίζες μιας κυβικής εξίσωσης, μέσω των τομών δύο κωνικών.
Η προσέγγιση του Καγιάμ είχε χρησιμοποιηθεί νωρίτερα από τον Μέναιχμο κυρίως, για την επίλυση συγκεκριμένων ειδικών περιπτώσεων κυβικών εξισώσεων και σε σχέση ακριβώς με τον διπλασιασμό του κύβου. Ο Καγιάμ ήταν ο πρώτος που γενίκευσε την γεωμετρική μέθοδο του Μέναιχμου ώστε να καλύψει ουσιαστικά όλες τις κυβικές. Μολαταύτα, με αρκετές “μεμονωμένες περιπτώσεις/αντιμετωπίσεις”, ώστε να αποφύγει τους αρνητικούς αριθμούς.
Αναφέρεται σε κάποιες σοβαρές πηγές και μελέτες , και είναι μάλλον γενικά αποδεκτό, πως ο Καγιάμ πίστευε λανθασμένα ότι η κυβική εξίσωση δεν μπορούσε να επιλυθεί αλγεβρικά, αλλά θεωρώ πως πρέπει να είμαστε πολύ προσεκτικοί στο να κάνουμε υποθέσεις σχετικά με το ότι μπορεί να αναφερόταν σε αυτό που συνιστά την σύγχρονη ιδέα μιας “αλγεβρικής” λύσης.
Μια από τις πιο διάσημες σχετικές ρήσεις του είναι:
“..Δεν πρέπει να δίνουμε μεγάλη σημασία στο γεγονός πως Άλγεβρα και Γεωμετρία είναι διαφορετικές στην εμφάνισή τους. Η Άλγεβρα είναι γεωμετρικά γεγονότα που έχουν αποδειχτεί!”
Αυτή η ρήση συνήθως “τεκμηριώνει” το πώς ο Ομάρ Καγιάμ συνέβαλλε στο “πάντρεμα-συμφιλίωση” των δύο τομέων, της Γεωμετρίας και της Άλγεβρας, που υπήρξαν τόσο αυστηρά διαχωρισμένοι από τους Έλληνες, και τον αναγάγει σε πρόδρομο του Ντεκάρτ…
Υπάρχει ασφαλώς κάποια αλήθεια σ’αυτή τη θεώρηση. Ο Καγιάμ ήταν σίγουρα πιο δεκτικός και “έτοιμος” από τους Έλληνες, στο να αντιμετωπίζει τα γεωμετρικά του τμήματα σαν “αριθμητικές ποσότητες” πιο πολύ,παρά σαν αυστηρά “χωρικές ,αφηρημένες οντότητες”. Και μάλιστα ανέπτυξε μια αριθμητική-υπολογιστική (“ευριστική” θα την λέγαμε ίσως σήμερα) εκδοχή της Ευκλείδειας (του Εύδοξου) θεωρίας της αναλογικότητας, η οποία προσεγγίζει πολύ τον ορισμό του Ντέντεκιντ (Dedekind) για τους άρρητους αριθμούς!
Ο Καγιάμ όμως, είπε αποδεδειγμένα και κάτι άλλο, πολύ σημαντικό για το θέμα μας.
“..Αυτή (η εξίσωση) δεν μπορεί να λυθεί με επιπεδομετρία , καθώς έχει έναν κύβο μέσα της. Για την επίλυση ,χρειαζόμαστε κωνικές τομές!”
Στο χωρίο του αυτό ακριβώς, μπορούμε να πιστώσουμε στον Καγιάμ την πετυχημένη πρόβλεψη περί της μη-επιλυσιμότητας του Δήλιου προβλήματος με “κανόνα και διαβήτη”, αλλά πιστεύω ότι ρίχνει και αποσαφηνιστικό φως στο υποτιθέμενα λανθασμένο πιστεύω του πως “η κυβική δεν μπορεί να λυθεί αλγεβρικά”.
Ας θυμηθούμε ότι γι’αυτόν “Η Άλγεβρα είναι γεωμετρία που έχει ΑΠΟΔΕΙΧΤΕΙ” και “Γεωμετρική Απόδειξη” για τον σίγουρα επηρεασμένο έντονα από τις αυστηρές ελληνικές νόρμες Πέρση σοφό, συνιστούσε ο “κανόνας και ο διαβήτης” . Αυτές ήταν οι “έγκυρες” αποδείξεις. Και τα τρία διάσημα αρχαία “άλυτα προβλήματα”, ο τετραγωνισμός του κύκλου, ο διπλασιασμός του κύβου και η τριχοτόμηση της γωνίας, ήταν ήδη γνωστό στην εποχή του ότι επιλύονταν με διάφορες γεωμετρικές μεθόδους, οι οποίες όμως ήταν “εκτός προδιαγραφών” και γι’αυτό θεωρούνταν -ως λογικές κατασκευές- κατώτερες. Οι ‘Ελληνες τις αποκαλούσαν “Μηχανικές κατασκευές” ,για να τις ξεχωρίσουν από τις αυστηρά Ευκλείδειες κατασκευές.
Έτσι, σε αυτά τα πλαίσια, μοιάζει μάλλον φυσική η δήλωση του Καγιάμ ,δεδομένης της θεώρησης σαν “έγκυρης” μόνο μιας θεωρητικής απόδειξης. Μιας αλήθειας που βασίζεται στο Ευκλείδειο αξιωματικό σύστημα (δηλαδή με “κανόνα και διαβήτη”). Με αυτή την ερμηνεία (και έχοντας πάντα στο μυαλό μας το “αξίωμά” του: “Άλγεβρα = αποδεδειγμένη Γεωμετρία) η περίφημη “λανθασμένη” δήλωσή του για την μη- επιλυσιμότητα των κυβικών είναι απολύτως σωστή, και κατ’ ουσίαν ήταν μια άλλης μορφής διατύπωση για το ότι το Δήλιο πρόβλημα δεν μπορούσε να λυθεί με κανόνα και διαβήτη.
Αλλά ας εμβαθύνουμε και λίγο στο “Γιατί;”, σε σχέση πάντα με το πρόβλημα του διπλασιασμού του κύβου.
Οι αριθμοί που μπορούν να κατασκευαστούν με κανόνα και διαβήτη ανήκουν σε διαδοχικά σύνολα (με σύγχρονη αλγεβρική ορολογία θα μιλούσαμε για “επεκτάσεις σωμάτων”), της μορφής:
K0 ⊂ K1 ⊂ K2 ⊂ K3 ⊂ K4 ⊂…Kν ⊂…
όπου τα στοιχεία του Κο είναι της μορφής α(ο) + β(ο)−−−−√ του Κ1, της μορφής α1+β1−−√, με α1, β1 να ανήκουν στο Κ0 και ούτω καθεξής. Σε κάθε σύνολο Κν δηλαδή, ανήκουν τα στοιχεία της μορφής: αν+βν−−√, με αν και βν να ανήκουν στο Κ(ν-1).
Σε καθένα από τα σώματα αυτά ,στα οποία ανήκουν οι κατασκευάσιμοι αριθμοί, περιέχονται λοιπόν γραμμικοί συνδυασμοί τετραγωνικών ριζών των στοιχείων των προηγούμενων σωμάτων, που στην ουσία περιέχουν ρίζες τέταρτης, όγδοης, κ.ο.κ τάξης. Οι κυβικές ρίζες λοιπόν, ΔΕΝ περιέχονται σε αυτά τα επεκτάσιμα σύνολα.
Το μαντείο ζήτησε έναν βωμό που δεν ήταν κατασκευάσιμος, γιατί δεν απαιτεί ούτε τετραγωνική, ούτε τέταρτη, ούτε γενικά καμία ρίζα άρτιας τάξης. Έτσι, ο αριθμός αυτός δεν βρίσκεται σε κανένα από τα διαδοχικά σώματα της μορφής Κν. Ο Απόλλωνας, μάλλον δεν το γνώριζε αυτό.
***
Γιώργος Ριζόπουλος – Λεμεσός, Ιούλης 2013
Πηγή: eisatopon
Σχόλια
